カタラン数 メモ

あらすじ

ネットをぶらぶらしていて、https://www.comp.tmu.ac.jp/masanori/Lecture/11discrete.pdf を見つけて読んだ。
カタラン数、名前は聞いたことがあったが真面目に追ったことはなかったけれど、PDFが分かりやすかった。

カタラン数

競技プログラミングにおける数え上げ問題について時々登場します。
自分も解けなかった問題のやり方を聞いたときに「あれはカタラン数というものがります」といわれてそんなのありかいと思った記憶があります。

カタラン数は計算過程が面倒なものの結果はとてもシンプルです。
というわけで実用的には、カタラン数が当てはまる性質を知っておいて結果を適当な所から引っ張ってこれるようにだけしておけばOK。

結果

c_n = \dfrac{1}{n+1} _{2n}C_{n}

とりあえず、結果だけ表示します。「これはカタラン数が答えになるはずだ」と分かっていればこの式を適用するだけです。

性質

カタラン数c_nは、次の漸化式を満たすもの。

c_n = c_0c_{n-1} + c_1c_{n-2} + ... c_{k}c_{n-k-1} + ... + c_{n-1}c_0 　( c_0 = 0 )　　

感覚的な理解として、以下のような問題であれば当てはまる。
- 分割する線をずらしながら二つの小問題に分けられる
- 分けられた二つの小問題はnが小さくなるものの元の問題と同じであり、再帰的に解ける


始めに紹介したPDFでも取り上げられている例ですが、たとえば(n+2) 角形に対角線を引いてn個の三角形に分割する場合の数は上の漸化式を満たします。(ただし n=0 を便宜上1通りとする)

(説明) 基準となる辺を一つ決めます f:id:socha77:20210322005923p:plain

頂点を一つ選ぶと領域が左右に分かれます 左右で分割の仕方は独立になっているので、分割iを決めたときの分け方総数は左右の積になります。

また加えて、各分割は重ならない(分割iと分割jに共通して現れる分け方がない) ので、最終的な答えは先に書いた漸化式で表せるということになります。 f:id:socha77:20210322010807p:plain

勘違い

勘違いというか、自分が整理する中で混乱した点ですが...

カタラン数のポイントを「分割して再帰的に解く」とだけ抑えていると、以下の過ちにハマる可能性があります(ハマった)。

  • 左右の分割の添え字の和は n ではなくて n - 1
  • それぞれの分割間で、共通して出てくる場合が存在してはいけない

三角形分割例で、たとえば以下のような考え方での分割をしてしまう可能性があります(誤り)。 f:id:socha77:20210322012549p:plain

この例では元のカタラン数のn = 8と比べて左右の分割のカタラン数の和(1+7, 2+6 ...) が減っていません。

ここで違和感なのですが、一番大きいのは各分割から共通してたどり着く分割方法があるということです。

f:id:socha77:20210322013226p:plain

というわけで、そもそも「重複して数え上げない」という数え上げの原則に違反するよろしくない考え方ということになります。

というわけで問題設定や添え字を適切に設定して正しい定義にフィットするようにしましょう。

適用例

見た目の異なる様々な数え上げ問題が実はカタラン数に帰着します。

ここまでで御託を述べましたが、正直初見でカタラン数であるということに気づいて正しく立式するのは難しい気がします(少なくとも自分には)

少なくとも競技プログラミングなどで使う用途であれば、具体例をたくさん覚えておく方が吉だと思います。身も蓋もない話ですが...
(初見で導くにしても、すでに持っている知識が多いほうが自分で埋めるべき考察の距離が短くなるはずです。)

以下のリンクなどから具体例を眺めてみて(、漸化式に当てはまるかを適宜確認してみて)ください。
急に雑ですみません
カタラン数 - Wikipedia

カタラン数の意味と漸化式 | 高校数学の美しい物語

カタラン数

中締め(？)

本当は証明を追っていて埋めるのに時間がかかった行間をメモするつもりだったのですが、いざカタラン数の話をしようとしたときに自分の中でまとまっていなかった点を整理していたら思いのほか時間がかかってしまいました。

もともとしようと思っていた話は別に回します。

ここまで見ていただきありがとうございました

Codeforces Round #699 (Div. 2) D. AB graph

あらすじ

Graphvizの練習　

問題概要

codeforces.com

n頂点の完全有向グラフが与えられる。
各辺には"a"または"b"というラベルがついている(辺 u→v と v→uのラベルは異なる場合もある。)

f:id:socha77:20210221005448p:plain

このグラフ上の経路で、通った辺のラベルをその順につなげたときに長さ mの回文になるようなものはあるか。
あれば構築して出力し、なければ"NO"と答える。

同じ辺を何回通過してもよい。

2 \le n\le 1000, 1 \le m \le 100000 (本当はマルチケースだけど省略)

続きを読む

ACL Contest 1 B - Sum is Multiple

あらすじ

atcoder.jp

解けて嬉しかったのと、解説と少し違ったのでメモです。

問題概要

整数Nが与えられる。1 + 2 + ... + k がNの倍数になる最小のkを求める。
1 \le N\le 10^{15}

考察の流れ

はじめに

N = 1の場合、明らかに答えは1です。
天下り的で申し訳ないのですが後々面倒なので、以降N ≧ 2として考えます。

まず

 
\sum_{i=1}^k = N \\\\
k(k+1) / 2 = N \\\\
k(k+1) = 2N

まず(整数の積) = 2N となっていることから、2Nを素因数分解するとよさそうです。

素因数の分割

とりあえず具体例を挙げながら考えます。
ひとまず、2N = 23 * 32 * 52 あたりにします。(N=900)
kの素因数とk+1の素因数は合わせて最低でも2を3個、3を2個、5を2個持つ必要があります。

ここで重要な性質としてkとk+1は差が1なので互いに素です。
共通の因数を持たないことから例えば2を両方に割り振ることができず、23を片方が持つ必要があります。

これを考えると(それぞれが少なくとも持つ)因数の割り振り方は

 1 vs 2^3*3^2*5^2,  2^3 vs 3^2*5^2 , ....  2^3*3^2*5^2 vs 1

で2 ^ (2Nの素因数の数) 通りになります。これらの分け方を総当たりします。

各分割の中での考察

前節で考えた割り振りの各パターンについて考えます。それぞれに割り振った素因数の積をx, y と置きます。 (例: x = 23*52, y = 32)
ax - by = 1 となるような自然数a, bでbyが最小になるようなものを見つける必要があります。

x と y は最大公約数が1のため、 ax + by = 1となるような整数の組 (a, b) は拡張ユークリッドの互除法で求めることができます。
以下、得られたxとy の符号で場合分けをします。

  • (a > 0 かつ b > 0) もしくは (a < 0 かつ b < 0)
    x ≧ 1, y ≧ 1 なので出現しません。 ax + by の値が 1より大きくなるか、負になるため
  • a > 0 かつ b < 0
    求めていた条件に一致します。-byがこの分割で得られる k として最適です。 条件を満たすa, b 自体は任意の自然数tに対して (a', b') = (a+ty, b-tx) でいくらでも得ることができますが、この解から得られるk' は k < k' のため最適ではありません。
  • a < 0 かつ b > 0
    (a', b') = (a+y, b-x) で a > 0 かつ b < 0 のパターンに持っていけます。(ここ少し不安なので、間違っていたらすみません...)
  • a = 0 または b = 0
    コーナーケースで、注意する必要があります。
    x, y の分割が 1と2Nになった時に、1 * 1 + 0 * 2N = 1という解が得られますが、ここから a > 0 かつ b < 0のパターンと同じようにk = 0と持っていくのは明らかに誤りです。
    分割が1と2Nの場合、k = 2N-1, k+1 = 2N とするのが最適です。 (片方が因数に2Nを持つ、差が1、積が2Nの倍数の中で最小のペア)

以上のいずれかで、分割を決めた中で最適のkを得ることができるので、これを他の分割から得られたkと比較して最小のものを出力します。

計算量

  • Nの 素因数分解に O(sqet(N))
  • 得られた p 個の数 [(素因数1)^{x_1}, (素因数2)^{x_2}, ... , (素因数p)^{x_p} ] を2つに分割する選び方は2^{p}通り
  • それぞれの分割で拡張ユークリッドの互除法を行うのにO(log(N))

で、 O(sqrt(N) + 2^{p}log(N))で解けるはずです。

pの雑な見積もり方ですが、素因数をp個持つ最小の自然数は、素数のうち小さい方からp個の積です。 p = 15程度でこの数は1015を十分に超えるので、p≦15として制限時間に間に合います。

終わりに

今回は色々回り道を試して答えにたどり着くことができましたが公式解説がかなり綺麗だったので、知識を付けてその力で問題を簡潔にするという方法もできるようになっていきたいなと思いました。 拡張ユークリッドの互除法に苦手意識がありましたが、けんちょんさんの記事

拡張ユークリッドの互除法 〜 一次不定方程式 ax + by = c の解き方 〜 - Qiita
の力を借りて解くことができたので苦手意識が減ったのは嬉しいですね。

間違いなどありましたらコメントもしくは @sentya7までお知らせください。 お読みいただきありがとうございました。

ABC189 E - Rotate and Flip 雑記

あらすじ

atcoder.jp

問題を解いたのですが公式解説に書かれていた知識を持っておらず、回り道をしていたので思考過程のメモをしました。
なお該当のコンテストには出ておらず、「線形変換」というキーワードは目にした状態でスタートしていました。

問題概要

二次元平面上にN個の駒 (x_i, y_i)が置かれている。
以下のうち一つを行う、という操作が合計M回行われる。

  • 平面全体を時計回りに90度回転
  • 平面全体を反時計回りに90度回転
  • すべての駒を x = pに対して対称な位置に移動
  • すべての駒を y = pに対して対称な位置に移動

Q 個のクエリに答える。

  • A回目の操作が行われた直後にB番目の駒はどこにあるか。

1 \le N, M, Q \le 10^ 5
10^ {-9} \le x_i, y_i, p \le 10^ 9

解法概要

各クエリに対してシミュレーションをすると間に合わない。
4つの操作は全て平面に対する線形変換なので、変換行列の積を取ることで複数回の連続する操作をまとめて1度の変換で行うことができる。

公式解説

Editorial - AtCoder Beginner Contest 189 を見てください

4つの操作はそれぞれ、 座標を表すベクトル (x, y, 1)^ T に対して


\begin{pmatrix}
0&1&0\\
-1&0&0\\
0&0&1
\end{pmatrix}
\begin{pmatrix}
0&-1&0\\
1&0&0\\
0&0&1
\end{pmatrix}
 \begin{pmatrix}
-1&0&2p\\
0&1&0\\
0&0&1
\end{pmatrix}
\begin{pmatrix}
1&0&0\\
0&-1&2p\\
0&0&1
\end{pmatrix}

(追記)

上の変換行列の導出を教えてもらいました。

同時座標系という手法を用いることで平行移動を(ベクトルではなく)行列で表現することができ、以下に書かれているのと同じような平行移動->対称移動->平行移動の操作を一つの行列にまとめることができる、という話でした。

自分の考察

※まず変換行列は2×2だと思っている

それぞれの変換が行列で表せれば累積積で各クエリに対して O(1)で対処できる

回転行列はわかるが、鏡写しの場合が分からない(ググったが雑過ぎて引っかからず)

x=pではなくy軸対称の変換なら


 \begin{pmatrix}
-1&0\\
0&1\\
\end{pmatrix}

で表せて嬉しい。

なので、一度平行移動により対称移動の軸がy軸と重なるようにして、上記行列を作用させた後に平行移動を元に戻す。

例: (2, -1) を x=3に対して対称な位置へ


(2, -1) - (3, 0) = (-1, -1)    \\\\

\\\\

 \begin{pmatrix}
-1&0\\
0&1\\
\end{pmatrix}
(-1, -1)^ T = (1, -1)^ T    \\\\

\\\\

(1, -1) + (3, 0) = (4, -1)

左右対称移動について一般化


A = 
 \begin{pmatrix}
-1&0\\
0&1\\
\end{pmatrix}
,
x = (x, y)^ T
,
b = (p, 0)^ T

として、移動後の座標を x'とすると


x' = A(x - b) + b  \\\\


   = Ax -Ab + b

変換前の座標に依存しない部分を -Ab + b = b'と定義して、 x` = Ax + b'

複数回の変換

y = p_1 を軸とした対称変換の後に y = p_2を軸とした対称変換をするとどうなるか


A_1 = A_2 = 
 \begin{pmatrix}
-1&0\\
0&1\\
\end{pmatrix}
,
x = (x, y)^ T
,
b_1 = (p_1, 0)^ T
,
b_2 = (p_2, 0)^ T

とする。(後々の一般化のために、A_1とA_2は別物としている)


A_2(A_1 (x - b_1) + b_1 - b_2) + b_2 \\\\

= A_2(A_1x - A_1 b_1 + b_1 - b_2) + b_2  \\\\

= A_2 (A_1 x - b'_1 -b_2) + b_2  \\\\

= A_2 A_1 x - A_2(b'_1 + b_2) + b_2

で結局、初期値を


A_0 = 
 \begin{pmatrix}
1&0\\
0&1\\
\end{pmatrix}
,
b_0 = (0, 0)^ T

とすると、 i 回目までのすべての変換による結果を表す行列およびベクトルは


A’_i = A_i A'_{i-1}  \\\\

b'_i = -A_i(b'_{i-1} + b_i) + b_i

の漸化式で表せる。

実装上は累積積(のようなもの)を保持する配列を2つ用意して末尾に逐次pushしていけばいいので、 M回分の操作に対してO(M)で前計算することができる。

4つの操作に対する一般化

前節までは左右対称の変化のみを扱っていたが、他の操作に対しても


A = 
 \begin{pmatrix}
0&1\\
-1&0\\
\end{pmatrix}
,
b = (0, 0)^ T  (時計回り) \\\\

A = 
 \begin{pmatrix}
0&-1\\
1&0\\
\end{pmatrix}
,
b = (0, 0)^ T  (反時計回り) \\\\

A = 
 \begin{pmatrix}
-1&0\\
0&1\\
\end{pmatrix}
,
b = (p, 0)^ T  (左右対称) \\\\

A = 
 \begin{pmatrix}
1&0\\
0&-1\\
\end{pmatrix}
,
b = (0, p)^ T  (上下対称) \\\\

と定義することでそのまま使うことができる。

前述のとおり O(M)で前計算し、Q個のクエリに対してそれぞれO(1)で答えることでACすることができる。

解答

Submission #19659845 - AtCoder Beginner Contest 189

(累積積を持っているということは、時刻 l - rでの変換を切り取るとかもできそうですが、逆行列がなかったりする場合もあるのかな)

免責

数学の議論とはてなブログの記法に疎いため、数式のふりをしたただのお気持ち表明が多くなっています、すみません。

ルービックキューブにおけるGod's Number解明までの歴史 さわりだけでも理解したい！

まえがき

こんにちは、煎茶と申します。

初めての方、はじめまして。

去年も見ていただいた方、ありがとうございます。

この記事はアドベントカレンダー 14日目の記事となります。

adventar.org

前日はNokiさんの ユリノキのパーフェクトすきゅーぶ教室

翌日は葉っぱの大学生さんの 場所法で手順を覚えてみた(Square-1 EP編) になります。

God's Numberとは何か

ルービックキューブを用いた競技としてもっともメジャーなのはどれだけ「速く」揃えることができるかというものですが、世の中にはどれだけ「短い手数で」揃えられるかという競技に取り組んでいる人々がいます。

その競技に関連して長いこと考えられてきた疑問が、「ルービックキューブを毎回最小手数で揃えられるとして、もっとも大変な場合は何手かかるのか？」というものです。全ての状態から最短で揃える全知全能の神というイメージから、この問題にはGod's Numberという名前が付けられていました。

最終的に、2010年になってルービックキューブはいくら大変でも20手以内に揃えられるということが明らかになり、この問題は終わりを迎えました。(God's Number = 20.) ネット上のメディアなどで取り上げられていたので、記憶にある方もいるかもしれません。

God's Numberは数学的な考え方と、計算機を用いた問題解決という2つの分野が混ざっているとても面白い問題です。 実際20手というのは、証明方法の改善と計算機の性能向上両方が合わさって達成された数字です。

実際20手の証明ってどんな感じだったのか？というのをなんとなく知ってもらうため、この記事では証明までの歴史および、おそらく公開されている中で最も古い証明方法の紹介を行います。

なお古い証明方法は「God's Numberは52手よりは少ない」というものであり、20手についての解説はこの記事では詳細には行いません。ご了承ください。(僕が説明できません)

この問題の面白さを知るきっかけになれれば嬉しいと思います。

補足: 「1手」とは？

今回扱うGod's Numberでは、HTM(Half Turn Metric)という基準で手数をカウントしています。HTMでは90°回転だけでなく180°回転も一手として扱います。

180°回転を2手として扱う指標はQTM(Quarter Turn Metric)と呼ばれておりQTM基準でのGod's Numberは26であるということが示されましたが、今回は扱いません。

また、M2などの中層を回す操作はL2 R2のように分解されて二手扱いされます。

God's Numberの歴史

20手の証明をしたグループが証明の概要およびそれ以前の20手への漸近の記録をドキュメントとしてまとめてくれています。 (http://cube20.org/)

このドキュメントには20手の証明の概要、過去に公開されたGod's Numberに関する年表、実際に20手かかるパターンはどれほどあるかといった統計資料などが乗っています。

年表を見ていきましょう。

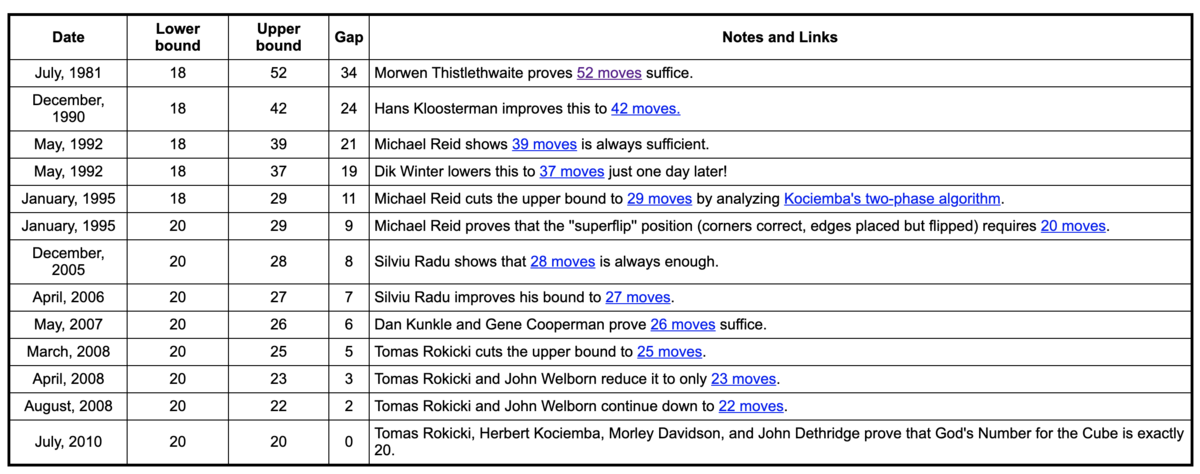
f:id:socha77:20201214110113p:plain
cube20.org より引用

God's Number 下界と上界

表のLower bound(下界)とUpper Bound(上界)という部分に注目してみます。 God's Numberは上界と下界から挟む形で求められました。
下界は比較的簡単なようで、早い段階で20手が下界ということがわかっていたようです。例えば初期は18手と言われていましたが、これは実際に18手以上かかる盤面を構成することでOKになります。(後々20手かかるパターンが見つかる)

一方で上界は全ての盤面が20手以下であると言わなければいけないので、難しいです。「今のところ見つかっていません」だと、まだあるかもしれないという不安が付きまといます。

それでは、上界を示すにはどうすれば良いのでしょうか？一番簡単な方法は、ルービックキューブのあり得る状態を全部試すことです。

探索の先駆け: Thistlethwaite

Thistlethwaiteは上記の年表に引用されている中でもっとも古く40年も前の文献ですが、20手に漸近していくまでの証明の根幹となる考え方が含まれています。

今でこそ52手というのは全く遠く思えますが、(おそらく)計算機を活用した方法を初めて発表したということで、大きな貢献だったのではないでしょうか。

以下に続く章では、計算機でルービックキューブをシミュレーションするというのはどういうことなのか、40年もかかるほどそれは難しいのか、そしてThistlethwaiteがどのように一歩目を切り開いたか、ということについて説明していきたいと思っています。

それではまず前提として、計算機でのシミュレーションに広く用いられる「探索木」という概念を、簡単な○×ゲームを題材に説明します。見たことある話だなと思う方は飛ばしてもらっても構いません。

○×ゲームの探索木

○×ゲームはお互いに最善な手を取れば必ず引き分けで終わりますが、本当かどうかを自分で確かめようとしたことがある方もいるのではないでしょうか？ 確かめる方法は簡単で、あり得る全部の分岐を試すのが良いです。

紙の上であり得る○×ゲームの試合を書き並べてダメかあと確認する代わりに、計算機の上でそれを行うための一つの手法が探索木という概念です。流れを以下に示します。

ゲームの任意の時点で切り取った盤面を一つの「状態」とします。(○を半分だけ書いたところ、とかはちょっと勘弁してくださいね)
具体例はこんな感じ。 f:id:socha77:20201214110219p:plain

注意点として、○の数が多すぎたり、ゲームが過去に決着している場合など不可能な状態もあります。また、どういうルートで盤面にたどり着いたかは無視してください。

ある状態からは、可能な手(遷移)を打つことによって次の状態を得ることができます。

f:id:socha77:20201214110515p:plain
{○, 6}などの表現はなんでもいいです。矢印に情報が乗っかっていることをイメージしてもらえると嬉しいです

以上を用いて、初期状態から遷移する9パターンを得る、得られた状態からさらに複数の遷移をして... という風に、手が打てなくなるまで場合わけを広げていくと、○×ゲームで起こりうる全ての状態を得ることができます。

f:id:socha77:20201214121751p:plain
探索木の一部分

それぞれのノードからエッジが枝分かれしているように見えるので、探索木と呼ばれています。

埋まっているマスが減ることはないのでこの探索技は不可逆で、いつか全てのノードが終了ノードにたどり着きます。 この網羅された探索木を使うことで、お互い引き分けに持ち込めるなどの○×ゲーム全体の性質を掴むことができます。 (探索木を用いたゲーム攻略は、例えばmin-max法やα-β法といった広がりがあります。)

この探索木はそのままオセロ、チェス、将棋、囲碁などにそのまま応用できます。(遷移は単純ではないですが)
しかし、まだ世の中には将棋や囲碁で100%勝てるプログラムは開発されていません。どうしてなのでしょうか？この話は後々説明します。

ルービックキューブの探索木

○×ゲームで考えた状態および遷移という考え方はルービックキューブにも同じように適用することができます。HTMでカウントされる任意の操作が「遷移」、そして0回以上の操作を加えたルービックキューブがそれぞれの「状態」を持っています。

f:id:socha77:20201214110926p:plain
エッジ単独反転やコーナー単独ツイストは各面の回転だけで行えません。

ということで完成状態を根として探索木を広げていきたいのですが、ルービックキューブは○×ゲームと違って終わりがありません。そこで、今まで通過した状態を全て記録し、既に見たことがある状態にたどり着いた場合はそこで打ち切りをすることにします。 今回探索木を作る目的なのはできるだけ短い手数なので、深い側にある方の頂点を遠回りとみなしてカットしてしまいましょう。

f:id:socha77:20201214110729p:plain
遠回りな方を打ち切りに

f:id:socha77:20201214124038p:plain

キューブの状態数は有限なので、この方針で全ての状態を網羅できそうです。 完成した探索木の最大の深さを調べれば、それがそのままGod's Numberになります。

素直な探索木の限界

さて、探索木を用いてシミュレーションをすることでGod's Numberを求められることがわかりました。おめでとうございます。

ところで、ルービックキューブのとりうる状態数ってどれくらいあるんでしょうか？ 答えは4325京2003兆2744億8985万6000通りです。指数表記ではおおよそ4.3 * 1019通り。

愚直にシミュレーションをしようとすると、これが大問題になります。

計算機には実は計算できる量に限りがあり、現在の一般的なPCだとおおよそ 109回/秒 程度の四則演算ができるようです。本当は回転をシミュレートしたり新しく発見した状態を記録したりする必要があるので無理なのですが、最大限楽観的に考えて1秒につき109通りの状態を新しく発見するとしましょう。すると網羅にかかる時間は...おおよそ1万年ほどでしょうか。

2100通りとかさらに無理な量の計算をやらせようとすることを俗に「宇宙滅亡」とかいう形で揶揄することがあるのですが、それに比べれば案外現実味のある数字に見えなくもないです。

もし現在もGod's Numberが解明されていなくて誰も解法を思いつけないのであれば、未来の人類に託してプログラムを回しておくのも一つの手です。今日やりましょう。

まあでも、自分が生きているうちに終わって欲しいですよね。そういう場合は別の手法をとる必要があります。

また、実は計算時間以外にも大きなネックになる部分があり、それは記憶容量です。 これも最大限楽観的に考えて、1つの状態を記憶するのに1bitしか使わないと仮定した上で大体40E(エクサ)byteくらいですか？個人の資産ではちょっと厳しそうですね。

将棋や囲碁で(今のところ)必勝法が見つかっていないのも、大体こういうことです。 理論的には最適な手を指すことができるが現実的には無理なため、様々な工夫によって勝てそうなルートを探索していくということです。

52手解法の説明

さて、この辺りから先述のドキュメントの内容に入っていきます。

まずは、どの流れで説明するか悩むので、概要を全て書き記します。ある程度知っている人であればここでわかるかもしれないですが、詳しい説明は後々続けていくので大丈夫です。簡単に目を通しながらスクロールしてください。

Thistlethwaiteのアルゴリズム

概要説明ここから

解法に先んじて、使用可能な回転の集合によってルービックキューブの状態を定義する表記について説明する。
例えば、<R>は完成状態、そこからR, R2, R'の4種類の状態の集合を表す。
同様に<L, R>なら3 * 3 + 1(完成状態)の10種類の状態の集合を表す。

筆者は、以下の4種類の状態を定めた。添字が大きい集合は、添字が小さい集合のsubsetになっている。

G_0 = <L, R, F, B, U, D>
G_1 = <L, R, F, B, U2, D2>
G_2 = <L, R, F2, B2, U2, D2>
G_3 = <L2, R2, F2, B2, U2, D2>
G_4 = I (完成)

先の章で述べた「ルービックキューブのパターン全部網羅」というのはG_0からG4への遷移を全て見つけることに等しい。

この解法では問題を以下の4つに分割することで、それぞれの問題のパターン数を減らし、現実的な計算時間で網羅することを可能にした。

G_0 -> G_1 EOを揃える 2,048通り
G_1 -> G_2 側面ステッカーを揃える 1,082,565通り
G_2 -> G_3 対面色のみにする 29,400通り
G_3 -> G_4 完成まで 663,552通り

それぞれの部分問題で、最も手数がかかったパターンを足すと、
7 + 13 + 15 + 17 = 52
よって、最悪でもルービックキューブは52手以内に完成する。

概要説明ここまで

改めて説明: 分割ステップその①

先ほどの省略しまくりの概要説明のことは忘れてもらって大丈夫です。

さて、探索木の問題は、枝分かれが多すぎる、深すぎる、そして埋めなければいけない状態数が多すぎることにありました。

というわけで少し天下り的なのですが、まずは一旦問題を簡単にして考えることにします。

ルービックキューブに、各面180°ずつしか回転をできないという縛りを加えたら問題はどう変化するのでしょうか？ とりあえずある状態から1手進め時の枝分かれが6通りに減ります。直前にあった動作はするだけ無駄なので、実質5通り。なんとなく木がすっきりしそうな感じはします。

180°の回転で得られる状態はどれも、「どのステッカーについても、同じ色もしくは対面色のセンターがある面に必ずいる」という特徴があります。(対面色...緑⇆青, 白⇆黄, 赤⇆橙。実際に何回か回してみるとわかるかと思います。)

このように対面色同士しかないキューブの状態全部をひっくるめた集合を、<L2, R2, F2, B2, U2, D2> と呼ぶことにします。<>に含まれる動作の組み合わせでたどり着ける物全部、という意味です。またこの集合にG_3という名前を付けます。何で3からなん？という点については後述します。

f:id:socha77:20201214110820p:plain

G_3は全部で663,552通りの小さな集合になり、全通り探索するという力技を行うことができます。(60万は元の1019通りから見ればとても小さいです。)

Thistlethwaiteさんはこの小さな問題を探索しきり、G_3からであればどれだけ遠くても17手で完成状態からどの状態にでも行けることを示しました。(実際にはコーナーを解いてからエッジを解くというふうにさらに分割していますが、詳細は省きます。)

めでたしめでたし。

問題を分割することの嬉しさ

さて本題より小さな問題は無事に解けたわけですが、これで何が嬉しいのか、ということを考えていきます。

ここまでで、G_3(「対面色同士しかない状態」の集合)に含まれる状態であれば、どこからでも(17手以内で)完成状態にたどり着くことがわかりました。

ということは、本題を「G_3に含まれるどこかにたどり着けばOK」ひいては「3色しかないルービックキューブだと思って全通りを探索できればOK」と言い換えることができます。(お手持ちのキューブで緑のステッカーを青に、黄色を白に、橙を赤に貼り替えてみてください。)

f:id:socha77:20201214113453p:plain

このように大きな問題を問題Aと問題Bに分けることで、Aのことを考えている間はBのことを忘れBのことを考えている間はAのことを忘れることができるというのがこの手法の大きな利点です。

f:id:socha77:20201214113337p:plain

最終的にThistlethwaiteのアルゴリズムでは全体を4つのステップに分割しています。

分割ステップその②

後ろ側(G_3 -> G_4)から説明を始めたので、次は(G_2 -> G_3)のステップについて説明します。

G_2はG_3と比較して、LおよびRの90°回転が解禁されました。 中層にあるエッジたち(UF/FU, UB/BU, DF/FD, DB/BD)は中層同士しか行き来できませんが、側面にあるエッジおよびコーナーは「元々側面のステッカーが側面を向いたまま」という縛りの中でどこにでも配置することができます。

f:id:socha77:20201214113521p:plain

このような状態は全部で29,400通りです。(ステップ①を既に行っているので、対面色は同じ色だと思って考えています。)

探索の結果、15手以内にこのステップの全パターンにたどり着けることがわかっています。

側面に接しているエッジやコーナーはどんな配置になっていても最悪17+15手で揃えられるので、同じ色(黒で表記しています)だと思ってしまっても大丈夫ですね。これで残った問題がまた簡単になりました。続きます。

分割ステップその③

続いて、G_1 にあって G_2にないパターンを探索していきます。 G_1 = <L, R, F, B, U2, D2> にできない操作は U, U', D, D'のみで、かなり自由度が高いです。

実際G_1でできないことは、「EOを変化させること」のみです。 EOの変化とは簡単にいうと、1つのパーツについている2つのステッカーを変換することです。

f:id:socha77:20201214113544p:plain

・コーナーパーツ/側面エッジパーツ/中層エッジパーツ同士を区別しない(G_2以降で揃えるので)
・全てのEOが正しい(G_1の条件)
を満たすのは全部で1,082,565通り、最長で13手かかります。

分割ステップその④

というわけで残った作業G_0 → G_1は「全てのパーツのEOを正しくする」です。 2,048通りで、7手以内で完了します。 ちなみに、このパートは人力でも慣れればできます。

Thistlethwaiteのアルゴリズム まとめ

というわけで、それぞれの分割問題が無事解けました。あとはそれぞれの問題を繋げれば、当初の問題であった「シミュレーションでルービックキューブの全パターンを網羅したい！」という問題の解になります。

G_0→G_4になるように辿れば、実際に崩れたルービックキューブを揃えていくことができます。

おさらいですが、

G_0 -> G_1 EOを揃える
G_1 -> G_2 側面用のステッカーを側面へ
G_2 -> G_3 前後/上下面のステッカーを対応するグループに
G_3 -> G_4 完成まで

となり、最悪でも 7 + 13 + 15 + 17 = 52 手です。

Thistlethwaite's 52-move algorithmには、実際に各ステップで全パターンを網羅したことの証明としてある状態からどう操作すれば完成状態に持っていけるかが列挙されています。(ただし、リストの解読が非常に難しいため実際にはほぼ無理かと思います。)

God's Number問題の発展

まえがきにも記した通り、この解法を発展させることでGod's Numberは20手に近づいていきます。 とりあえずというか、問題の分割を

G_0 = <U, F, R, L, B, D>
G_1 = <U, R, F>
G_2 = <U, R2, F2>
G_3 = I

のようにすることで39手まで縮まるようです。(http://www.math.rwth-aachen.de/~Martin.Schoenert/Cube-Lovers/michael_reid__new_upper_bound.html)

またその後も、同様に問題を分割してルービックキューブを解くTwo-Phase Algorithm を発展させて... というふうにして手数は縮んでいきます。自分の理解がたらずこれ以上は説明できないのですが、興味があればぜひ cube20.org を覗いてみてくださいね。

なお、Two-Phase Algorithmについては今年のアドカレ2日目で2006NISH01さんが解説されています。ぜひ読んでみてください。

qiita.com

あとがき

ここまでお読みいただいたみなさま、ありがとうございました。

今更になって謝罪しなければいけないのですが、今回に自分の記事は結構不完全な可能性があります。

cube20.org の存在を知り、これ面白そうだから他の人にも知ってもらいたい！！という思いとともに勢いで登録をしたものの、思ったより読解と整理が進まずギリギリ提出クオリティになってしまった... というのが私の言い訳になります。

また、ルービックキューブは計算機科学だけでなく数学、特に群論のテーマとして扱われることが多く群論の知識があればもっと簡潔かつ正確な説明ができたのではないか... とも思っています。

ということで、間違いを発見したり違った視点による理解をお持ちの方がいればバンバン指摘していただければ...と思います( )

最終的に言いたいのは、God's Numberの話題ってすごく面白い！！しかも文献にアクセスすることができる！というのを皆さんに知ってほしかったです。今日の話は全部忘れても、cube20.org の存在は覚えて帰っていただければ幸いです。

(おまけ: この記事があがる一週間ほど前に、キューブ系YouTuberである J Perm がGod's Numberに関する動画をアップロードしていました。自分は彼のファンなのですが、今回ばかりはタイミングの悪さに涙を流しています。)

www.youtube.com

それでは、これで本当に終わりとなります。繰り返しになりますがお読みいただきありがとうございました。また機会があればどこかで。

CodinGame Fall Challenge 2020 参加記

CodinGameで開催されていた Fall Challenge 2020に参加しました！

Fall Challenge 2020って何？というかたは、こちらの記事を参考にしてください。

tsukammo.hatenablog.com

要約

  • 初めてヒューリスティクス的なコンテスト/コンペに参加しました
  • Silverリーグまで行けました 嬉しい～～
  • Goldも行ってみたかった / ビームサーチとかをこの機会に学びたかったけど失敗 次も参加したいね

f:id:socha77:20201124004822p:plain

あらすじ

(~11/12)
Twitterでこどげのイベントがそろそろ、みたいな発言をちょくちょく見つける
興味あるけど難しそうだし、自分はパスかな...

(11/13)
Twitterに参加者の所感が出始める

  • 実在のボードゲームを題材にしてるっぽい
  • なんか絵柄がシュール

まあ... (メールフォルダを開く) f:id:socha77:20201123233011p:plain

やるか～～～～～～～～～～～～～～～～～～～～～～～～～～～～

Wood League

(11/13) サイトを開く。Errichitoさんがなんか実況してる動画をみる。実況動画のアドバイスに従い、適当に BREW ${ID}を出力する。
Wood 2 → Wood 1昇格 嬉しい～～～～

以降、最後まで基本戦略は「できるだけ早くBREWをする」で固定です。

さて、コードを書き換えて
何かしらBREW > 何かしらCAST > REST
の順に優先順位をつけて行動させるようにしました。

すると、ポーションを1, 2個作って動作停止して負けるパターンが見受けられました。調べます。
どうやら、
level 0 生成 → level 1に変換 → level 2に変換 → level 3に変換 → level 0 生成 → ....
を無限にやっていたようです。

画面には10個のlevel 3素材を格納したインベントリと動作停止した婆が映っていました。あほくさ 同じ素材は3個まで、みたいな縛りを追加すると良い感じに回りました

Wood 2 → Bronze昇格 嬉しい～～～～

Bronze League

さて、ランダムに呪文を唱えていても当然勝てません そもそも急にルールが難しい...

こういうコンテストでの探索手法とかが全く分からないので、普段の競プロ的アプローチでできる手を取ります。

問題: 現在の状態(インベントリ、呪文、ポーション) から、最も短いターンで何らかのポーションをBREWできるルートを見つける

相手のことは全く考えていませんでした(余裕がない)
あと3ターンでとれるルートを走っていたら次ターンでとられて台無し、という危険性もありますが、しょうがないと割り切り毎ターン計算しなおしています。

この問題は、インベントリの状態ごとにたどりつける最短ターン数を記録しておくDPで解くことができます。
( インベントリの状態 ... [Level 0, Level 1, Level 2, Level 3] = [2, 2, 1, 1] とか [0, 0, 3, 3] とか、そういうこと )

計算量は 状態数(10 ** 4) × 選択可能な呪文の数(せいぜい20とか) × 探索を打ち切るターン数(10ターン以内に無理ならLEARNをするようにしていました) 程度です。

その後、多少のバグ取りをしてアリーナに放出すると、対戦結果がポコポコ出はじめて楽しい！
ですがBronze上位3割くらいにとどまり、う～んという感じに

適当に情報取集をすると、呪文のなかでもアドであるものとそうであるものがあり、初期の呪文はかなり弱いとのこと。
レベルの低い素材から 1, 2, 3, 4点として変換効率考えると、確かに...

ということで、最初の数ターンはLEARNに専念させることにして提出。
したのですが、バトル結果は勝率5割くらいで振るわなそう？うーむ

疲れたのでこの日は諦めることにしました。

1時間ほどYouTubeを見て、寝る前にメールをチェックします。

f:id:socha77:20201124002652p:plain

？？？

Bronze → Silver昇格 嬉しい～～～～～～

Silver League

どうやらビームサーチというもので戦える！ということを聞いていたので、Silverに上がったらすっぱり切り替えようと思っていました。

ですが、Bronzeまでの手法にもまだやれそうなことがあり(一番顕著なのはRepeatableを1回ずつ唱えているところとか)、調整していたところバグの沼に.......

ビームサーチの勉強に使おうと思っていた時間を溶かし、撤退することになりました。

まとめ

ひとまず始めたときはSilverを目標にしていたので、達成できて嬉しいです。

この機会にビームサーチを勉強しよう作戦は失敗してしまったのですが、これは次のイベントまでの宿題に。

元々日本勢が盛り上がっているという話は聞いていたのですが、Twitterでこどげのことをつぶやくと参加者リストに入れてもらったり、実際に参加する側の空気を感じることもできて楽しかったです。

次はGold目指してリベンジしたいですね～～

それでは、ここまでお読みいただきありがとうございました！

ランダムケースデバッグのすすめ (camel_case)

競技プログラミングを嗜む人間が例外なく頭を悩ませるもの、それはコーナーケース

主要コンテストサイトでは大体1ケースのWAで0点にされ、ここからが労力の残り半分みたいなシチュエーションもままある

N = 1のパターン一つくらいなら(特に1ケースWAなどで示唆されていれば) 見落とす可能性は低いが、2つ3つと考慮すべきケースがた場合すべてを網羅するための注意力は並大抵では済まない

________ じゃあ、テストケースの全部がコーナーケースみたいな問題があったら ...？

atcoder.jp

続きを読む